How To Find Gcd Of Two Numbers

Java Program to Find GCD of Two Numbers

In this section, we have covered different logics in Coffee programs to find GCD of 2 numbers.

Greatest Common Divisor: Information technology is the highest number that completely divides 2 or more numbers. It is abbreviated for GCD. Information technology is also known as the Greatest Common Factor (GCF) and the Highest Common Factor (HCF). It is used to simplify the fractions.

How to Find the Greatest Common Factor

Write all the factors of each number.
Select the mutual factors.
Select the greatest number, equally GCF.

Instance: Discover the GCF of 12 and eight.

Solution:

Factors of 12: ane, 2, three, 4, 6, 12

Factors of 8: one, two, 4, 8

Common Factors: 1, 2, 4

Greatest Common Factor: 4

Hence, the GCF of 12 and viii is 4.

Algorithm to Find GCD

Declare two variables, say 10 and y.
Run a loop for 10 and y from 1 to max of x and y.
Check that the number divides both (x and y) numbers completely or not. If divides completely store it in a variable.
Divide the stored number.

In Java, we tin use the post-obit ways to discover the GCD of ii numbers:

Using Coffee for loop
Using while loop
Using User-Divers Method
Using the Euclidean Algorithm
Using Modulo Operator

Using Java for loop

In the following programme, we accept initialized ii numbers ten=12 and y=eight. After that, we have used a for loop that runs from 1 to the smallest of both numbers. It executes until the condition i <= x && i <= y returns true. Within the for loop, we have besides used if statement that tests the condition (10%i==0 && y%i==0) and returns true if both atmospheric condition are satisfied. At terminal, we have store the value of i in the variable gcd and print the aforementioned gcd variable.

FindGCDExample1.java

Output:

Using Coffee while Loop

In the following instance, we take used while loop to test the status. The loop executes until the condition n1!=n2 becomes false.

FindGCDExample2.java

Output:

In the to a higher place plan, we tin supervene upon the while loop with the following logic that gives the same output.

FindGCDExample3.java

Output:

Using User-Defined Method

In the following program, we have defined a method named findGCD(). It contains the logic to find the GCD of two numbers. We have parsed two parameters a and b of type int.

FindGCDExample4.java

Output:

Enter the Beginning Number: 75 Enter the Second Number: 125 GCD of 75 and 125 = 25

Using the Euclidean Algorithm

The Euclidean Algorithm is an efficient method to compute GCD of two numbers. It is too known every bit Euclid's Algorithm. The algorithm states that:

If A=0 and then GCD(A,B)=B, since the GCD(0,B)=B, and nosotros can get out from the algorithm.
If B=0 then GCD(A,B)=A, since the GCD(A,0)=A, and we tin can exit from the algorithm.
Write A in the quotient that we get from (A=B*Q+R).

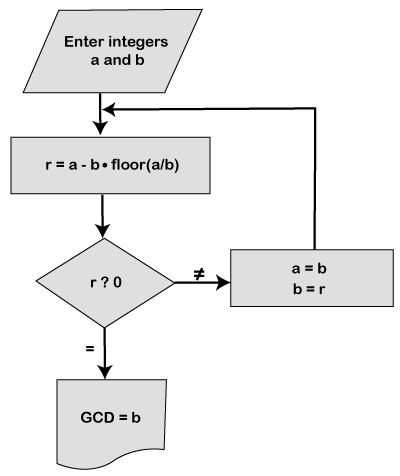
Java Program to Break Integer into Digits

Allow's implement the above logic in a Java program.

FindGCDExample5.coffee

Output:

Enter the two numbers:  11 33 The GCD of 2 numbers is: 11

Using Modulo Operator

In the following program, we have divers a recursive function named findGCD(). It parses two parameters a and b of type int. If the second number (b) is equal to 0, the method returns a as GCD, else returns a%b.

FindGCDExample6.java

Output:

Permit's see another logic to notice the GCD of two numbers.

FindGCDExample7.coffee

Output: